Путём несложных математических преобразований приведём ряд Тейлора к следующему виду:

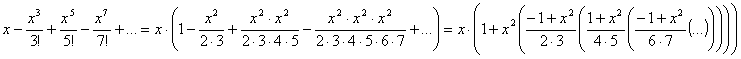
Получившуюся в результате схему можно представить в виде следующего выражения:

sinx=x+x³·recursive(x,glubina)

 

Рекурсивная функция recursive должна возвращать некоторое определённое значение. При бесконечной рекурсии мы получим максимально точное значение синуса. Но так как мы не можем использовать бесконечную рекурсию, мы должны ограничить её определённым количеством вызовов-погружений, то есть значение переменной glubina не должно превышать какого-то заранее определённого значения max_glubi. Это и будет условием внутреннего вызова рекурсии.

Так как мы хотим считать ряд "с конца", нам нужно в рекурсивной функции сначала осуществлять внутренний вызов, а потом уже считать выражение.

 

Function recursive(x:real;glubina,max_glubi:integer):real;

Var tmp:real;

Begin

  tmp:=0;

  if glubina<max_glubi then tmp:=x*x*recursive(x,glubina+1,max_glubi);

  if (a mod 2) = 0 then tmp:=(1+tmp)/(a*a*4+a*2)

  else tmp:=(-1+tmp)/(a*a*4+a*2);

  recurs:=tmp;

End;

 

Перед подсчётом значения синуса надо привести значение угла к величине от –пи/2 до пи/2:

 

Function Cut_int_pi(x:real):real;

var tmp:real;

Begin

  tmp:=pi*( x/pi-trunc(x/pi) ); { So we have 0 <= tmp < Pi. }

  if abs(trunc(x/pi) mod 2)=1 then tmp:=-tmp; {So we have -Pi<= tmp < Pi.}

  if tmp<-pi/2 then tmp:=-pi-tmp; { So we have -Pi/2 <= tmp < Pi. }

  if tmp>pi/2 then tmp:=pi-tmp; { So we have -Pi/2 <= tmp <= Pi/2. }

  Cut_int_pi:=tmp;

End;